Correcting the encoder filter frequency
Way back in 2021, I described the approach moteus uses for filtering encoder values and its derivation from the “all-digital phase locked loop”. What I did not realize until now was that the formulas used in that derivation operated based on the “natural frequency” of the filter, not the 3dB cutoff frequency as I had intended. They are related by a constant, but this resulted in the bandwidth of the encoder being higher than expected. Here, I’ll set the record straight, and document how that effects moteus going forward.
TLDR: Now moteus has slightly less audible noise for the same effective control performance. Read on for the details.
Background and derivation
The key problem was that in my derivation, I wrote:
$$K_p = 2 \zeta \omega_{3dB}$$
$$K_i = {\omega_{3dB}}^ 2$$
Whereas in Robertson’s original article he wrote:
$$K_p = 2 \zeta \omega_n$$ $$K_i = {\omega_n}^ 2$$
The key distinction being that ω_n is the “natural frequency” of the filter, where the response peaks, not the “3dB” or “cutoff” frequency, where the response is attentuated by 3dB, or one-half power.
To derive the 3dB frequency, I’ll work from an s domain version of the digital PLL. The closed loop transfer function of a second order PLL is:
$$C_L(s) = {{K_P s + K_I} \over {s ^ 2 + K_P s + K_I}}$$
We can substitute in the Robertson formulation of K_P and K_I to get:
$$C_L(s) = {{2 \zeta \omega_n s + \omega_n ^ 2} \over {s ^ 2 + 2 \zeta \omega_n + \omega_n ^ 2}}$$
For a test frequency ω, substitute jω in for s and take the magnitude squared which yields:
$$|C_L(j \omega)| ^2 = {{(2 \zeta \omega_n \omega)^2 + \omega ^ 4} \over {(\omega_n ^ 2 - \omega ^ 2) ^ 2 + (2 \zeta \omega_n \omega) ^ 2}}$$
If we define:
$$r = {\omega \over \omega_n}$$
Then we get:
$$|C_L(j \omega)|^2 = {{(2 \zeta r) ^2 + 1} \over {(1 - r^2)^2 + (2 \zeta r) ^2 }}$$
The 3dB point is where the magnitude is equal to 1/2.
$$2 (2 \zeta r)^2 + 1 = (1 - r^2)^2 + (2 \zeta r) ^2$$
Solving for r yields:
$$-r^4 + (2 + r \zeta^2) r^2 + 1 = 0$$
Let:
$$x = r^2$$
gives:
$$x^2 - (2 + 4 \zeta ^2) x - 1 = 0$$
Solve for x with the quadratic formula:
$$x={{2 + 4 \zeta ^2 + \sqrt {(2 + 4 \zeta^2)^2 + 4}} \over 2}$$
and now solving back for r:
$$r = \sqrt {{2 + 4 \zeta ^2 + \sqrt {(2 + 4 \zeta^2)^2 + 4}} \over 2}$$
We had originally used ζ=1.0, so that means the relationship between the 3dB and the natural frequency is:
$$r = {\omega \over \omega_n} \approx 2.48$$
Verification
To make 1000% percent sure that this is now correct, I made a simple tool that applies a sine wave to the encoder software at varying frequencies, and measures the amplitude of the response. It also plots the “ideal” response as computed by the s domain transfer function.
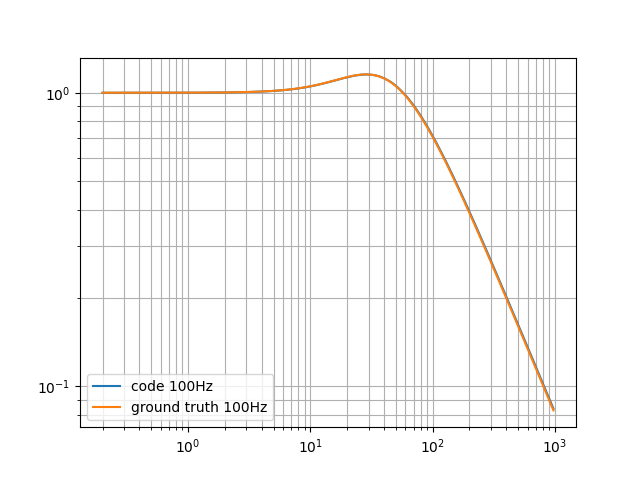
pll_filter_hz=100Hz
You can see that the response reaches roughly 0.707 at 100Hz, which is the 3dB cutoff point and that the code nearly exactly matches the ground truth transform.
Upshot
Previously, if the encoder low pass filter bandwidth was configured at 100Hz, that meant the 3dB cutoff frequency was actually 248Hz. This is in contrast to the torque control PI filter where the specified cutoff frequency is actually the 3dB point. We don’t need the encoder bandwidth to be that much higher than the torque bandwidth and this certainly wasn’t desired.
So, as of firmware release 2025-07-21, moteus has switched to the intended behavior where the configured PLL frequency is actually the 3dB frequency. A few things fall out of that.
moteus_tool --flashwill automatically upgrade or downgrade configurations as necessary when upgrading or downgrading firmware to maintain identical semantics.moteus_tool --calibratenow defaults to--cal-bw-hz 200. That sets both the torque control bandwidth and the encoder bandwidth to 200Hz, which results in roughly similar performance as the old default, with slightly less noise.
Ultimately, this means that with the default calibration parameters, you’ll get slightly less audible noise for the same effective control performance as less of the audible noise is wasted on a mismatch between the encoder bandwidth and the torque bandwidth.
